美術室
ここはアートの部屋だよ。
特に数学とアートというテーマでいろんな作品を展示しているよ。
アートは人生そのものかもしれないね。
ゆらぎを持つ離散力学系
ロマネスコカリフラワ ー
スクラッチボードグラフィティ
マゴと遊べるかなと思って100均でスクラッチボード(6枚入り)を買ってきましたが、マゴはどうやら興味なし!。なので、私がやってみたらおもしろ~い。割り箸の先をとがらせたようなスティックで「けがく」だけ。下描きなしの一発勝負ですが、何を描いてもアートっぽくなります。作品というほどではないのですがいくつか紹介しますね。
①いろいろなしもまっち
最初の作品。結局この絵しか描けないのです(笑)


②自己回避型ランダムウォーク
一筆書きで自己回避というルールを決めて筆の赴くまま描いていきました。描きながら、るんびにい美術館の小林覚さんの気分になって、秘かに文字を入れてみました。

③ヒルベルト曲線
ある数学の本の原稿締め切りに追われているとき気分転換に描きました。原稿のテーマが「自己相似」だったので、ヒルベルト曲線という自己相似図形にチャレンジしました。平面上の格子を自己回避の一筆書きで網羅する平面充填曲線なので格子の細かさを0に近づけたとき、フラクタル次元(ハウスドルフ次元)は平面と同じ2次元になります。一発で描くと失敗しそうですが、描いているうちに「入れ子」の感覚が得られるので何とか最後までいけました。
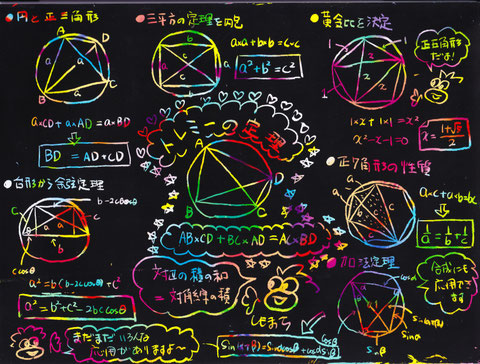
④トレミーの定理あれこれ
ある日、異常に早く寝たところ、翌朝異常に早く起き、なぜかその時ハマっていたスクラッチボードで数学のノート的なものを作ろうと思い、夢見心地でしゅしゅしゅっとトレミーの定理について速攻で描いて、またフトンに入った。そしたらもっかい眠ることができ、たくさんの夢を見た。至福だった。何だったんだろう。あの発作のような出来事は。

⑤積率母関数
あるワークショップに参加した時、面白いアクティビティがありました。それは、A,B,Cの3つの商品があって、その中から自分が欲しい物を1つ選び、その「念」を受け取って何を選んだかを当てるというものでした。6人に対して行ったのですが、最初の3人はハズレ、残りの3人はズバリ的中だったので会場が「おお!」となりました。さてこれは凄いことなのか。そのときちょっと計算してみました。独立試行なので、6人中ちょうど3人当たる確率は160/729(約0.22)、3人以上当たる確率は233/729(約0.32)なのでなかなかのものですね。因みに二項分布に従うと、平均=6×(1/3)=2、標準偏差=√6×(1/3)(2/3)≒1.15なので、平均±標準偏差は0.85~3.15。3回的中はシグマの範囲とはいえ、その上の方なので素晴らしいということで。自宅に帰って二項分布の平均と標準偏差ってどうやって求めるのが早いかなと思いながら、なぜか手元にあったスクラッチボードに積率母関数から平均と分散を求める方法を思い出して書いてみました。

⑥ミトコンドリア号
最後のスクラッチボードを見つけたので、「栄養素が細胞でエネルギーに変換される図」を描いてみました。4年ほど前、畠山さゆりさん(惣兵衛社長)の「断食マイスター養成講座」で得難い学びを経験しました。「食養生」と「幸せに生きる」というテーマについて、楽しみながら学ぶ中で、生科学への知識や興味関心が生まれ、高校時代大の苦手だった生物の勉強を見直したくなりました。授業もこのような動機づけをしながら展開できればと自問したものでした。そのときの私のメモしたノートからスクラッチボードに描きなおしてみたものです。
わざわざこんなスクラッチシートに書かなくても、普通にノートにかけばいいじゃん、といわれそうです。
ちっちっち。そうじゃないんですよ。こうやってお絵かきしてアソブからこそ、モチベーションとインタレストが生まれるんです。そして成果物を一人鑑賞してニンマリするんです。
ということで皆さんもチャレンジしてみては。
ガウスの整数環
もう30年以上前ですが、「複素数の素数の図示」が話題になったことがあります。いわゆる、ガウスの整数環における既約元の判定法です。例えば5は整数上では素数ですが、ガウスの整数環上では(2+i)(2-i)と因数分解されますね。当時私は複素数の素数にハマり、プログラムを作って遊んだり、ガウスの整数を通して、高校生に代数系に興味を持ってもらうためのテキストを作ったりしていました。エクセルで描画した図はこちらです。
ガウスの整数に関心のある方は「図書館」の部屋にファイルがありますのでそちらをご覧ください。

この画像をワードに貼り付けてみると面白い遊びができます。
図1は、2枚の画像をずらして重ねたもの。同心円が浮かび上がります。

図2は一方の画像を少しだけ縮小して重ねたもの。今度は渦巻きが見えます(もちろんガウスの整数である必要はなく、ラダムドットでできます)。これは以前、西山豊先生(大阪経済大名誉教授)から教えていただいた不動点定理を見える化したものです。西山先生はTPシートの重ね合わせでやったのですが、こうしてワードでも作ることができます。

塗り絵シリーズ
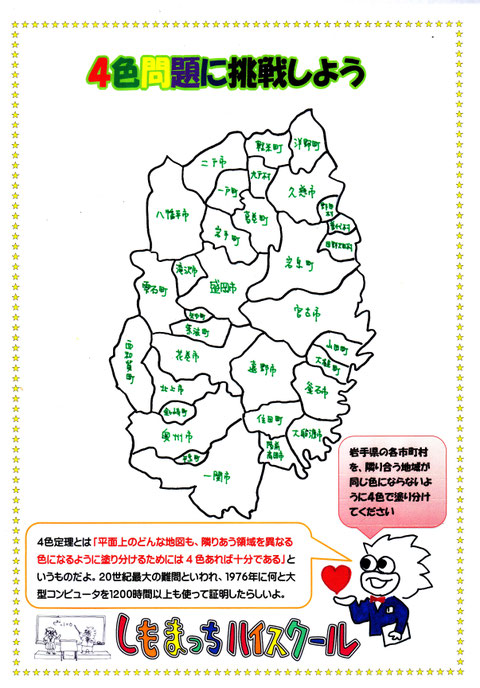
4色問題

素数塗り分け
ヘキソミノパズルの世界

ヘキソミノ=Hexsomino=Hexsa-Omino とは、正方形(Omino)を6個繋げて作られる図形です。ちなみに、正方形を2個繋げてできる図形はドミノ、3つはトロミノ、4つをテトロミノ、5つをペントミノといいます。ヘキソミノは図のように全部で35種類あります。

これらの35個のピースを、図のような「へそ」のある図形に全部を埋め込むというのがヘキソミノパズルです。
入れ方の総数は何億通りもあるのですが、それほど簡単ではありません。
私は小学生の頃からこのパズルにハマっていて、かなり多くの解をコレクションしてきました。でも、ただ埋め込むだけでは面白くなくなってきて、1分以内で作るとか、解の中に面白い図形を折り込むとか、変形パターンの多い解を作ることを試みるなどして遊んでおりました。
広島に中原克芳さんというすんごいパズリストの友人がおります。彼も私同様(私以上)ヘキソミノパズル愛好家です。
2000年に、幕張メッセで行われた国際数学教育者会議(ICME9)に、共同で、「ヘキソミノパズルにおける数理」と題してポスタープレゼンテーションしたことがなつかしい思い出です。そのときのアブストラクトは私の旧ホームページにあります(こちら)。
中原さんこそヘキソミノアーティストで、様々なユニークな作品を作られています。その彼が、以前私に「下町」の文字が入った解を作ってくださいました。そこで私も自分の名前の「壽」と「男」を頑張って入れてみました。ご覧ください。
「壽」は14画なのでかなり難しかったです。壽に見えますか。
ヘキソミノアートの世界は奥が深いですよ。ぜひ皆さんもチャレンジしてみてください。



ブログ「あなたと夜と数学と」でヘキソミノパズルについて書いたものを紹介します。
- ヘキソミノパズルの紹介。広島の中原さんの作品を中心に紹介しています。
- ヘキソミノパズルによる図形の拡大の話です
- 北海道の田村さんのアイデアとその作品について2度書いています。 ① ②
