一昨日の授業で、教科書にある次の活用問題をとりあげました。

因みに私はジャケットなどを紳士服のコナカでよく買いますが、2着買うともう1つ付けるとか、ズボンをつけるとかのサービスがあります。素直で人の良い?私は、店員さんに上手にのせられていつもたくさん買っちゃいます。
では問題を解いてみましょう。Tシャツ1着の値段をX円とすると、A店は30%引きなので、X-0.3X=0.7X円が1着の値段です。すると4着で2.8X円になりますね。一方、B店では3着だけ買えば4着もらえるので、値段は3X円です。
例えばTシャツの値段が1000円なら、A店では2800円、B店では3000円です。つまり、A店で買った方が2割ほどトクということになりますね。
問題はこれで終わりですが、授業ではさらに、もっといっぱい買った場合はどうなるのかという話しをしました。例えば5着買うとすると、A店では3.5X円、B店では4着買えばいいので、4X円です。やはりA店がよさそうです。では6着だとどうでしょう。
A店では0.7X×6=4.2X円です。B店では5着買えばいいから5X と言いたいところですが、もし、2着ずつ2回に分けて購入すればどうでしょう。2着+2着はプラス1着がそれぞれ付くので、結局6着ゲットできます。すると、値段は4X円なので、B店で買った方がトクであることがわかりました。
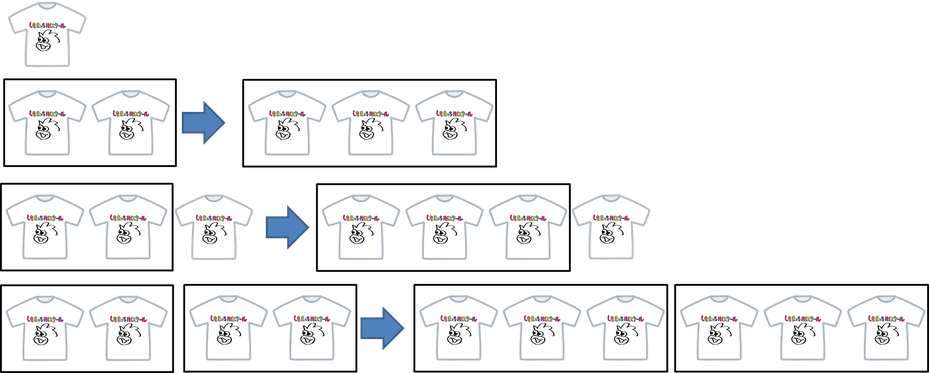
購入数を増やしていった場合それぞれのお店の値段はどのように変わるのか気になりますね。授業では、6着までしか考えませんでしたが、今朝一人でちょっと考えてみました。
まず、B店では2着以上でプラス1なので、2着を1セットにして、分割購入すればできるだけ多くのTシャツがゲットできるはずですね。この「2着→3着」ルールによって、1着から10着まで購入した場合の、ゲットできる最大数を表にしてみましょう。

10着買うと15着になるわけですね。因みに、A店で15着買うと、0.7X×15=10.5X円なので、B店の方が0.5ポイント得であることがわかります。

では今度は、A店とB店の金額の比較を表にしてみましょう。ここではTシャツ1着の値段をX円ではなく1とすることにします。
とりあえず、ゲット数30までについて調べてみました。B店は基本的に3つの場合に分けて考えればよさそうです。
(1) ゲット数が3の倍数の場合
ゲット数が3,6,9,・・・つまり、3Nの場合は、A店の金額は2.1N円で、B店は2N円なので、いつでもB店が得であることがわかります。
(2) ゲット数が3で割って1余る場合
ゲット数が1,4,7,10…つまり、3N-2の場合は、A店の金額は
0.7×(3N-2)=2.1N-1.4 となりますが、B店は奇数の列、つまり、2N-1となります。
この大小をグラフで比較してみましょう(左下図)。
N=4、つまり10着以上ゲットしようとする場合はB店が得ということになりますね。

(3) ゲット数が3で割って2余る場合
ゲット数が2,5,8,・・・つまり、3N-1の場合は、
A店の金額は 0.7×(3N-1)=2.1N-0.7ですね。
今、例えば、17着買いたい場合(N=6のとき)、A店では17×0.7=11.9円ですが、B店では「2着を何セットかと1着」という買い方ではちょうど17着にすることはできません。なぜなら、このような買い方は、必ず3k+1という数になるからです。そこで、B店でちょうど17着にするには、1着・15着→16円、3着・3着・3着・3着・1着→13円などいろいろ考えられますが、この時、3N-1個より1個多い3N着買うことにすると、B店での金額は2N=12円となり、ちょうど3N-1着買うより明らかに安くなります。そこで、ゲット数が3N-1着の場合は、B店の3N着と比較することにします。2.1N-0.7=2N から閾値を求めると、N=7つまり、20着のとき両者は等しくなり、N>7のとき、B店の方が安くなります。
つまり、20着以上買いたい場合はB店へ、ということになりますね。ただし、2着ずつを何度も分けてレジに持っていくのはとても勇気がいることなので現実的ではないですね。
まあ、何となく大学入試共通テストに出てもいいような問題ではあります。

コメントをお書きください