考えることの面白さを伝えたい

来週、遠野高校の生徒たちのあるメンバーに「数学って何？/数学の楽しさや考えることの面白さとは」というテーマでお話しをすることになっています。探究活動の取組みとして、地域の小中学生に算数・数学の面白さや考えることの楽しさを伝えたいので、そのヒントが欲しいとのことでオファーをいただきました。

そこで、考えることを楽しむ問題を一つ作ってみました。次のような問題です。

もちろん試行錯誤していけば解にたどり着くと思います。でも私は、問題を解くだけではなく、解決する戦略を考える中で整数の性質を理解してもらいたいという思いで作題しました。

どうすればエレガントに解決できるでしょう。皆さんも考えてみてください。

【解説】

ではちょっと理屈っぽく解説したいと思います。

■部屋割り論・全単射

まず、１～９の異なる9個の数を9カ所に入れるので、A～Iはすべて異なる数になることがわかりますね。つまりこの問題は、｛1,2,･･･,9｝から{A,B,C,･･･,I}への1対1の対応を考えるということです。

■かけ算から考える

まずG×H＝Iから考えるのがポイントです。A～Iは一桁の数なので、GHはかなり絞られます。

■単位元の性質

まず、G=1はあり得ません。なぜなら、１×H＝Hとなり、HとIが同じ数になってしまうからです。ここで、1を乗法に関する単位元といいます。

■背理法

また、Iが一桁の数であることを考慮すると、Gは2しかありえないことがわかります。なぜなら、もしGが3以上だとすると、G<H なのでIの最小値は3×4＝12と二桁の数になるからです。このように、あることを仮定して矛盾を導く証明方法を背理法といいます。

すると、GHIの組み合わせは2×3=6と2×4=8の2種類しかないことがわかりました。

■偶奇の和

ここで、(G,H,I)=(2,4,8) の場合を考えましょう。このとき、残った6つの数は1,3,5,6,7,9の6個です。注目するのは偶数6の存在です。この6個の数を3個ずつの２つのグループにすると、6が入るグループと、6が入らないグループに分かれます。6が入らないグループは3個の数がすべて奇数です。ここで、奇数＋奇数＝偶数、奇数－奇数＝偶数であることに注意します。このことから、3個の数がすべて奇数のグループはあり得ないことがわかりますね。以上から、(G,H,I)=(2,4,8) の場合はあり得ないことがわかります。

■和の組合せ

すると、A～Fには1,4,5,7,8,9が対応します。ここでは蛇足になりますが、これを３つずつ２つのグループに分けたとき、もし4と8が同じグループにいると、もう一つのグループは全部奇数になるので、２つのグループは4を含むものと、8を含むものに分かれます。

さて、では答えを求めていきましょう。(A,B,C)について考えます。Cがオーバーフローしない組合せは、①1+4=5 , ②1+7=8 , ③1+8=9 , ④4+5=9 の4通りです。そしてそれぞれに対して、(D,E,F)の組合せはⅠ(7,8,9) ,Ⅱ(4,5,9) , Ⅲ(4,5,7) , Ⅳ(1,7,8)が対応します。このとき、Ⅰ,ⅢはD－E=Fという形にできないので、①－Ⅰ、③－Ⅲは不可です。

ⅡはE<Fを考慮すると、9－4=5、Ⅳは8－1＝7とできますね。

以上から、求める答えは②－Ⅱ、④－Ⅳの2種類ということになりますね。

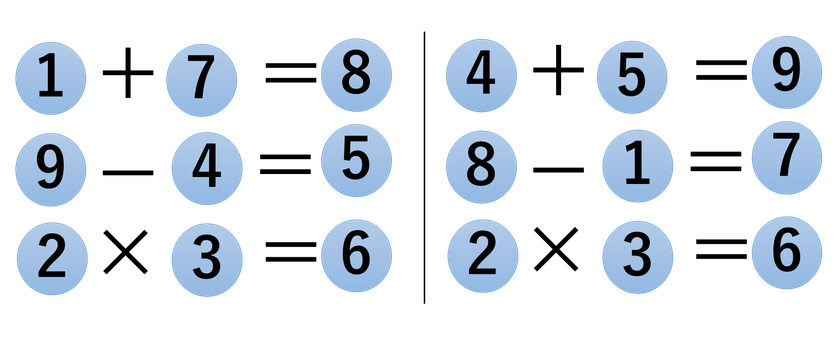
ちなみに、②－Ⅱと④－Ⅳは(A,B,C)と(D,E,F)を入れ替えたもの、いわばデュアル（双対）な関係です。

この問題は小中生を対象としたものですが、少し難しいものをやりたいという方は、次の問題はどうでしょう。

これだと、9+8≡7なども成立するので解が増えそうですね。