パソコンで立方体を描く

前回のブログでは１９９６年に行った古い実践の中から、三角形の外接円を描くプログラムについて紹介しました。この記事の肝は、パソコン上で任意の三角形の外接円を描くプログラミングの中に、高校数学で学ぶ三角比の公式がほぼすべて網羅されているということです。当時私は「空間における６つの結合公理がデザルグの定理一つの中にまとめられているということと同じように、三角比の内容を消去したものが外接円を描くプログラムなのだ！」などと欣喜雀躍した覚えがあります。まあ、少し大げさな話ではありますが、でも、学んで得た知識を俯瞰したり活用するためのひとつの方法として、このようなプログラミングは有効な手段ではないかと思うのです。

さて、では今回もそのような内容について書いていきたいと思います。これも前回同様、1996年にある雑誌に寄稿した記事のもので、空間図形をパソコン上にどうやって描画するかというものです。空間図形の把握にはパソコンの利活用が有効だと思いますが、逆に空間図形をパソコンに図示するためのプログラムを考えることで数学の有用性を実感しようという話しであります。古い内容ですがおつきあいいただければ嬉しいです。

パソコン上に立方体（正六面体）を図示して、自由に動かすようなプログラムを考えようと思います。3次元の物体を平面（2次元）上に移す変換としてもっとも簡単な一点透視法を用いることにします。下図１のように、リアルな正六面体があり、それを視点Eから眺めます。視点と物体の間にスクリーンを置きます。これがパソコンのディスプレイにあたります。ここで、視点と物体を結ぶ線分がスクリーンを切ったところがスクリーン座標になります。このスクリーンに映った像がいわゆるバーチャルな世界での正六面体ということですね。視点は物体のある実際の座標のｚ軸上にとり、スクリーン座標を、リアルのｘｙ平面と平行にとっておくことにします。

このようにすると、スクリーン座標は、下図２のような三角形の相似関係から

となります。この変換がリアルからバーチャルへの通行手形になるわけです。些細ではありますが、こんなところにも数学の有用性を感じて欲しいと思います。

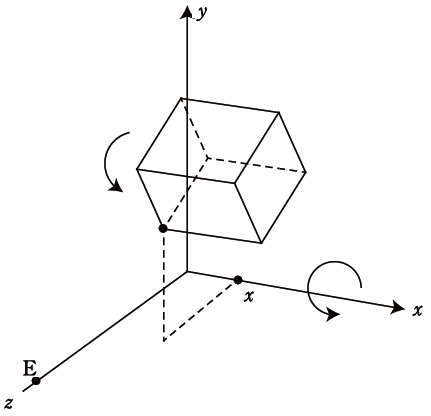
基本的に3次元空間上の動きは合同変換、つまり回転移動と平行移動を行うということですね。ではまず、x軸、y軸、z軸周りの回転移動を考えてみましょう。例えばx軸周りにθ回転させるということは、X座標は変化がなく、座標（Y,Z）を回転移動した点に変換すればいいですね。つまり、次のような回転行列によって決定することができます（下図参照）。y軸周り、z軸周りも同様ですね。

どうすれば裏の面を判定することができるでしょうか。私が最初に考えたのは、下図のように、「視点と立方体の各面の重心との距離を計算して、そのうちの短い順に３つの面だけを表示する」というものでした。

理由は、空間上の立方体は最大でも３つの面しか見えないし、見える面は視点に近いものであると思われたからです。

しかし、この方法でプログラミングして動かしてみると、殆どの場合はうまくいくのですが、立方体は視点からいつでも３つの面が見えるわけではないので、例外が発生してしまいます（下図参照）。

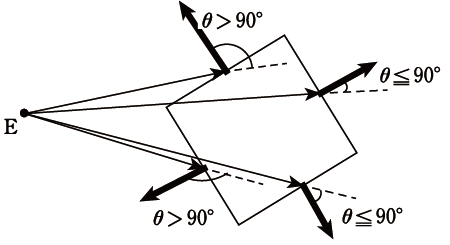
そこで、第二の方法として、図のように視線と立方体の各面との作る角度で判断するという考えが浮かびました。具体的には、視点から各面の重心を結んだベクトルと、各面の法線ベクトルの作る角が90°より大きければそれは見えない面であり、90°以下であれば見えない面と判断するという方法です（下図参照）。

因みに、後にパソコンのグラフィックに関する本を読んでいたら、同じような方法が載っていました。私の発見は初めてのものではなかったことを知りちょっと残念に思ったのですが、まあ、やはりこれが自然な考えということなのでしょうね。

この考えをどうプログラムに取り入れていくかというと、やはり数学の力が必要になってきます。２つのベクトルの作る角の大きさを判断するにはベクトルの内積を計算し、その符号を調べればいいですね。プラスなら鋭角、マイナスなら鈍角です。

また、平面の法線ベクトルは、外積を用いることで決定します。外積は高校数学を少しはみ出しますが、四面体や平行六面体の体積を求める場合に、法線ベクトルの話をされている先生もいるのではないでしょうか。

外積の求め方について次の例題で説明しましょう。

【例題】3点A(0 , 0 , 1),B(1 , 2 , -6) , C(-1 , 1 , 2) を通る平面の方程式を求めよ。

余談ですが、ここで求めた法線ベクトルの大きさはABとACの２つのベクトルが張る平行四辺形の面積になります。なので、平面ABC上にない点Dがあるとき、AB,AC,ADで張られる平行六面体の体積は、ADベクトルと法線ベクトルの内積になりますね（図参照）。さらにいうと、これは、３つのベクトルAB,AC,ADで表される3次の行列の行列式の絶対値になります。

以上で準備完了です。実際のプログラムのソースはあることはあるのですが、なにしろこれは20世紀の実践なので、言語が

Ｎ88BASICでありまして、残念ながら今は再現できないのです。悪しからず。

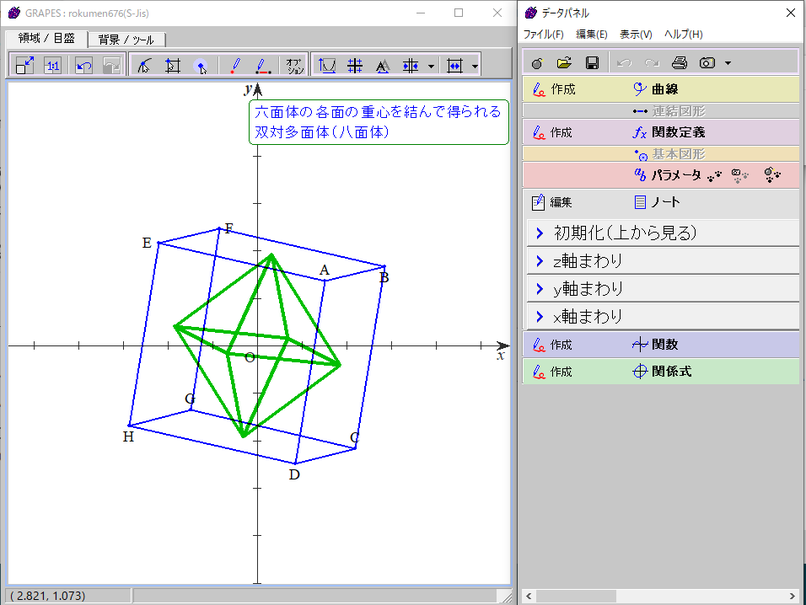
その代りGRAPESのスクリプト機能を駆使して作った立方体を描画するセッションを紹介します。陰線処理はしていませんが、各面の重心を結んでできる双対多面体も描画するようにしてみました。