東大文系数学添削講座より④　ヘロン三角形で遊ぼう

今回は、2006年の東大の問題を題材にしながら、三角比や図形についての基本性質をおさらいしてみたいと思います。

取り上げるのは次の問題です。

正弦定理と余弦定理しか使っていませんが、数が膨らむので、素因数分解の形で考えていく方がいいですね。また、2次方程式の性質（解と係数の関係）を使いながら求めていくところが面白いですね。そういえば今年（2022）の共通テストの三角比の問題は、2次関数の最大最小問題につながっていましたね。

この問題では４つの辺の長さと1本の対角線の長さがわかりました。すると、残った一つの対角線ACの長さも求めたくなりますよね。円に内接する四角形では、4つの辺と２つの対角線の6つの要素のうちの5つがわかっているときは、トレミーの定理を使うといいですね。トレミーの定理は「対角線の積＝対辺の積の和」という、とてもシンプルな形で表される式なので、以下のように簡単に求めることができます。

四角形の辺と対角線の長さが決定されたので、今度は面積を求めたいですね。△ABCは辺の比が13:14:15になる有名な三角形で、これは3:4:5型と、5:12:13型の２つの三角形がドッキングした形です。この三角形は3辺と面積がすべて整数になりますね。このような三角形をヘロン三角形といいます。では四角形ABCDの面積をまずは次のようにして求めてみます。

四角形ABCDを分割する２つの三角形△ABC，△ADCの3辺がそれぞれわかっていますから、ヘロンの公式を使って求めることもできますね。ヘロンの公式とは次のようなものです。

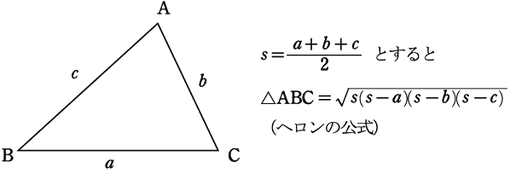
では面積を求めてみましょう。

ヘロンの公式の四角形版の公式がプラーマグプタの公式です。これを使えば一発で求められますね。

この問題では、外接円の半径が与えられています。これを用いて次のように三角形の面積を考えることもできます。

では２つの三角形の面積を求めてみましょう。

今回の問題では、対角線BD以外は整数になりました。美しいですね。でも、せっかっくだから、全部を整数にしちゃいましょう。全体を5倍すればいいですね。

5倍された四角形ABCDは次のように直角三角形に分割されます。分割するにあたっては、右下図のようなピタゴラス数を作る式が役に立ちます。例えば、ｍ＝8，ｎ＝１とすれば63:16:65の直角三角形が得られますね。

つまり上の図形において、△ACEと△ADFが3:4:5のタイプ（m=2,n=1）、△BECが5:12:13のタイプ（m=3,n=2）、△CDFが16:63:65のタイプ（m=8,n=1）の直角三角形になっているんですね。

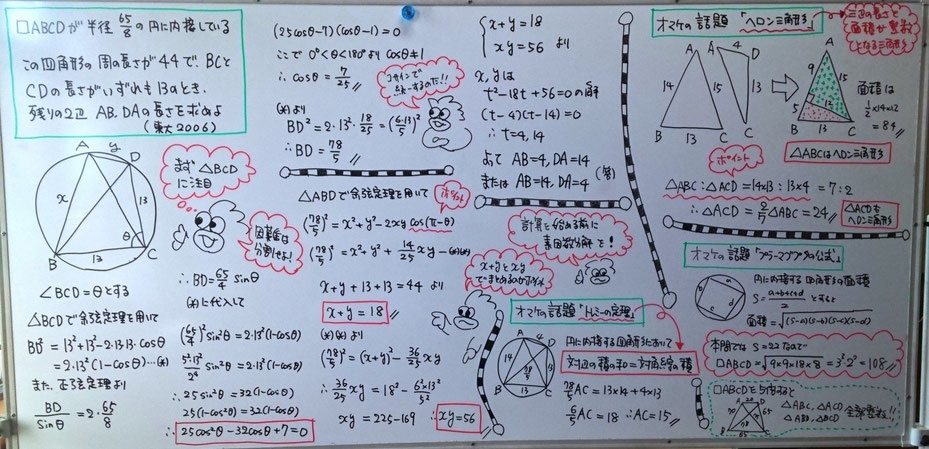
以上、ここまでの内容は、以前添削指導でホワイトボードに記したことをまとめたものです。最後にそのときのホワイトボードの写真をあげておきます。