親亀子亀三角形で三角関数の勉強

今年に入ってから、「インスタ数学」では大学入試共通テストを意識したコンテンツを配信しています。今日は、三角関数の様々なタイプの問題を一度に概観できる図を取り上げました（下図参照）。

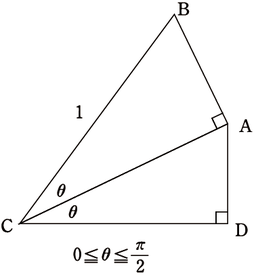
BC＝１で、∠BCA＝∠ACD＝θ，∠BAC＝∠ADC＝90°という条件を満たす図です。私はこれを「親亀子亀三角形」と呼んでいて、いつもセンター試験前に生徒に提示していました。

では、この図形を使っていくつかの問題をやっていきましょう。

まず、それぞれの辺の長さをθを使って表しておきましょう。

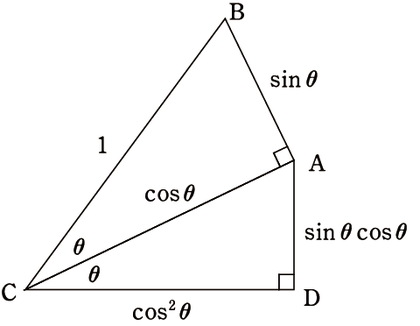
どの辺も瞬時にわかる感覚が必要です。三角比をいつまでも

という「sct図」で刷り込まれていてそこから抜けられない人がいます。この見方だけではなく、次の図のような見方が自然にできるように教師は適切なタイミングで生徒に示していく必要があると思います。

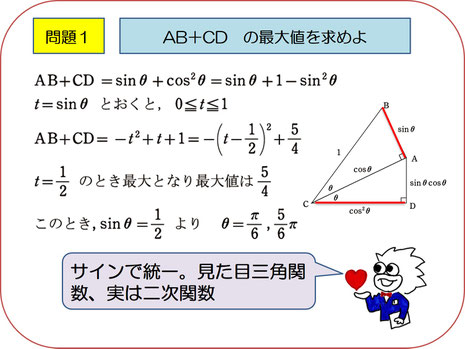
ではAB＋CDをθで表してみましょう。左の解答にあるように、sinθについての2次式で表せるので、これは2次関数の最大値を求める問題に帰着しますね。

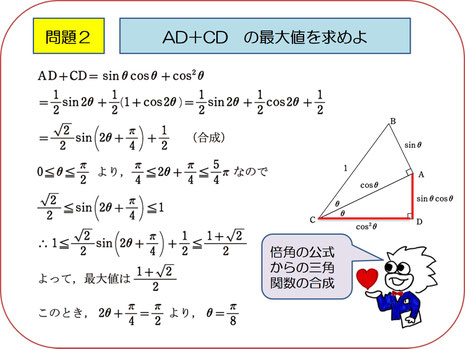
今度はAD＋CDをθで表してみましょう。

sinθcosθと、cosθの2乗の和になります。これは三角関数の定番問題で、sinθcosθをsin2θで、cosθの2乗をcos2θで表して、それらを合成してひとかたまりにしていくのですね。

更に、θが 5π/12 などのときのAD＋CDの値を求めるなどの問題も加えておいてもいいかと思います。

次に、AB＋AC+ADの最大値を考えましょう。これまた定番問題で、sinθとcosθの和と積が登場するタイプ（差でもよい）ですね。t=sinθ+cosθ とおいて、２つのことをします。

一つは両辺を2乗して、sinθcosθをtの式で表すこと。

もう一つは合成して、tの範囲を決定することです。

問題の続きとして、θが π/12 のときAB＋AC+ADの値を求めるなどの問題も面白いかと思います。

図では問題３となっていますが、問題４です。

この問題では余弦定理でBDを求めると、cosθの4次式になるのですが、3次と1次の項がないので、複二次式に帰着します。つまりcosθの2乗をtとおくと、tの2次式の問題になるわけですね。

最大になる角が有名角にならないところが面白いなあと思いました。

こんな感じで、共通テストを受ける前に目を通してもらえればと思ってブログにもあげておきました。

皆さんもやってみてくださいね。