二乗比例法則

今回のワンポイント講座では、2次関数における「２乗比例」という重要性質についてまとめてみたいと思います。

このような2乗比例の法則は、ガリレイの示した落体の運動や、速度とエネルギーなど、様々な自然現象に見られるものです。

では、このことを念頭において、2次関数の重要性質を導いてみましょう。

私がいつも授業で行っている、2次関数の2乗比例則を知るためのめっちゃカンタンな実験にについて述べたいと思います。

用意するのはカーテンレール（くの字に曲げておく。また、黒板にくっつくようにマグネットシートを貼っておく）

①　１当たり量を決める

パチンコ玉を何回かレールから発射させます。玉が落下するときのどこか1点を観測して印をつけます。（下写真①）

②　２のときの位置を予測する

１当たり量から、２のとき４となる場所に、小さなケースを置いておきます。玉を発射させると、予想したポイントにストライク！（下写真②）

③　３のときの位置を予測する

今度は、３のとき９の位置ををとります（目分量で十分）。玉を発射させると、用意していた小箱にストライク！自然現象を数学が解明しました！（下写真③）

実際の授業での動画をご覧ください。

因みに、下左図のように、頂点Oと1点Aだけがわかっている放物線があるとします。この放物線を皆さんはどれくらい正確に描くことができるでしょうか。恐らく多くの生徒は、2次関数の対称性から、Aのｙ軸に関する対称点は取るところまではできると思います。では、それ以外の点はどのようにとることができるでしょうか。これこそ、このカーテンレールの実験が役に立つところではないかと思います。下右図に１・４・９の規則をいくつか適用させたものを描きました。このように考えていけば、正確な放物線を描いていくことができますね。

多くの教師は、2次関数の描画について「頂点とその近くの2つくらいの点を取って、後は対称性に注意しながらそれを滑らかにつなげ」という指導をしているように思います。しかし、このような指導では2乗比例の性質がわからないままになってしまうような気がします。2次関数の描画では対称性や凸性とともに、2乗比例にもしっかりフォーカスしておく必要があります。カーテンレールの実験は、単なる興味を喚起するための教材ではなく、次に説明する2乗比例に関する重要公式に向かうためのものであることを強調しておきたいと思います。

カーテンレールの実験を踏まえて、2次関数の2乗比例則の重要公式について説明をします。下図の左は比例法則で、１当たり量が決まれば、それに対して、横がｌ 倍になると、縦も ｌ倍になります。2次関数は、下図の右の様に、1当たり量が決まれば、それに対して横が ｌ倍になると，縦はｌの2乗倍になります．

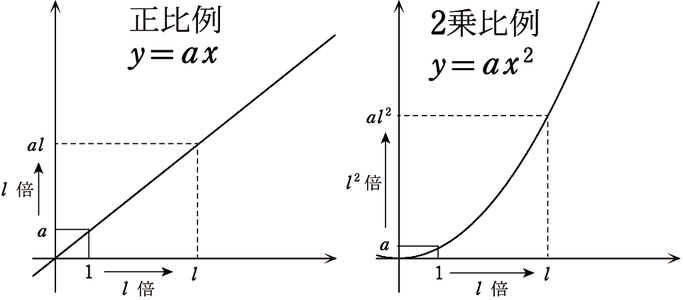
このことから、2次関数ではｘ軸と平行な直線を切り取る長さと、頂点までの距離に関して次のような重要な性質が導かれます。

では、上で述べた関係式の威力を実感する問題をいくつか取り上げてみたいと思います。

これに対して私は、次のように答えています。

これを受験テクニックを磨くスペシャルな公式として捉えるのではなく、2乗に比例する関数の基本性質として理解しておくということです。だからこそ、カーテンレールの実験をやったのです。2乗比例の性質と理解しておけば、別にこの式は、特別なものではなく、ごく自然で当たり前のものであると感じるはずです。