昨年の中学校での冬期休業中、「アドバンス数学」という課外講座を担当しました。学年の枠を取っ払うというユニークなコンセプトで、考案した担当者が苦労して、全部で30近い講座が立ち上がりました。私の講座は難しい内容を含むとアナウンスしていたので、まあ、数学の得意な3年生が5人くらい集まればいいかなと思っていました。ところがメンバーを見ると、何と1年生から3年生まで30人を超える希望者がおりました。そこで、何をやろうか頭を捻り、最初の2日間は数学史とピタゴラスの定理(三平方の定理)の話をし、最終日は名城大の竹内先生にヘルプをお願いして数論の話をしてもらいました。
というわけで、そのとき私が行った三平方の定理の内容について思い出しながらまとめてみたいと思います。
3:4:5の直角三角形
課外のオープニングに「3辺の長さの比が3:4:5の三角形は直角三角形になることを誰もが納得するように格子に図示せよ」という問いを設定しました。グループで相談しながら見つけることができたようです。


余談ですが、このように三角形を描くと、タンジェントが1,1/2,1/3であるような3つの三角形が浮かび上がって来て面白いです。この話題はまた後で。

三平方の定理を速攻で証明する
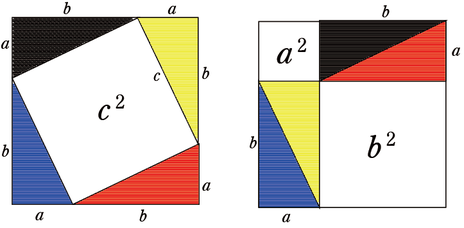
三平方の定理は優に100を越える証明があるといわれますが、1年生にも手っ取り早く納得してもらえるものとして、次の図で示しました。一つ目はこれ。白の部分の面積の比較です。図形を作ってホワイトボード上で三角形を移動して説明します。証明というより「納得」ですね。
上のことと似ていますが、代数計算を使って確認すると下の図のようになりますね。


面積比で考える
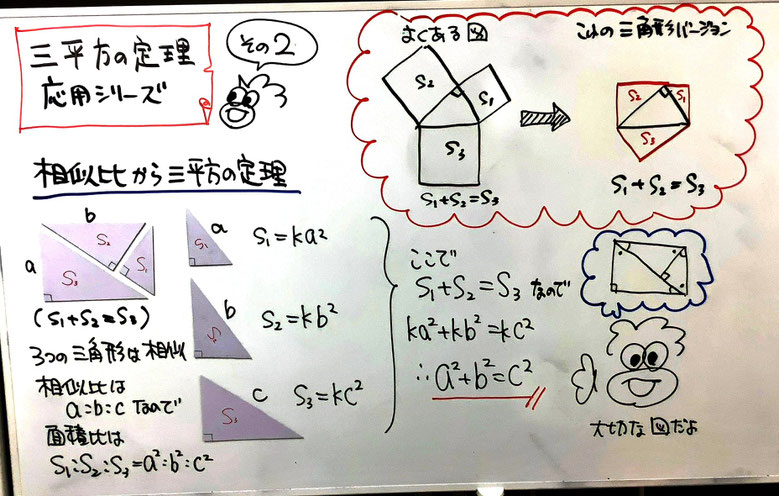
面積比が相似比の2乗になることを使って納得するという方法も示しました。「史上最低のジグソーパズル」といわれる教具があります(小沢健一氏による)。3枚の三角形の板によってできている長方形を別の長方形にするというものです。私は小沢先生からこれを紹介されたとき、三平方の定理の説明にちょうどいいと思いました。三角形の各辺に正方形を描いた図はよく見るのですが、相似の図形であれば正方形である必要はないですね。これは、正方形の代わりに三角形を描いたものになります。以下のホワイトボードの板書をご覧ください。
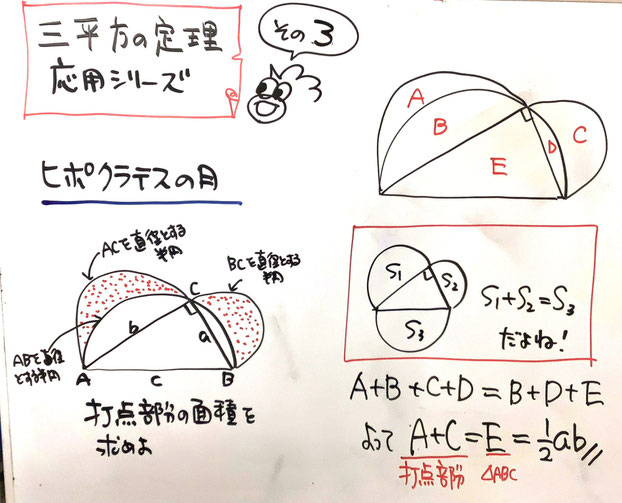
ヒポクラテスの月
各辺の上に半円を描いても、それらは相似なので、面積は小+中=大が言えますね。この考えを使ったヒポクラテスの月という問題も示しました。
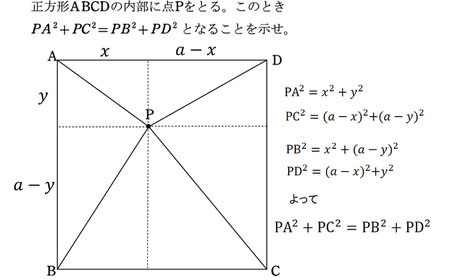
実践問題①
三平方の定理の威力を示す問題です。点Pが正方形内のどこにあっても成り立つところが嬉しいですね。高校生だったら、中線定理で考えたり、座標や複素数で考えたりなどいろいろ試してみればいいのではないかと思います。

実践問題②
今度は少し難しいです。右がヒントの図です。∠CDE=90°なので、ABとDEが平行となり、四角形ADBEは等脚台形になるところがポイントです。


実践問題③
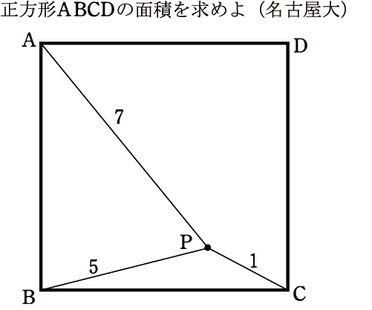
実践問題①を使った応用問題です。名古屋大の入試問題とのことですが本当かな。だとすると答えがしゃれていますね。
以下に板書の解説をあげておきます。

おまけの話題
三平方の定理の応用として、地震の震源地を求める話などがあります。今回は特殊相対性理論における時間のずれという定番のお話をしました。以下がその板書です。
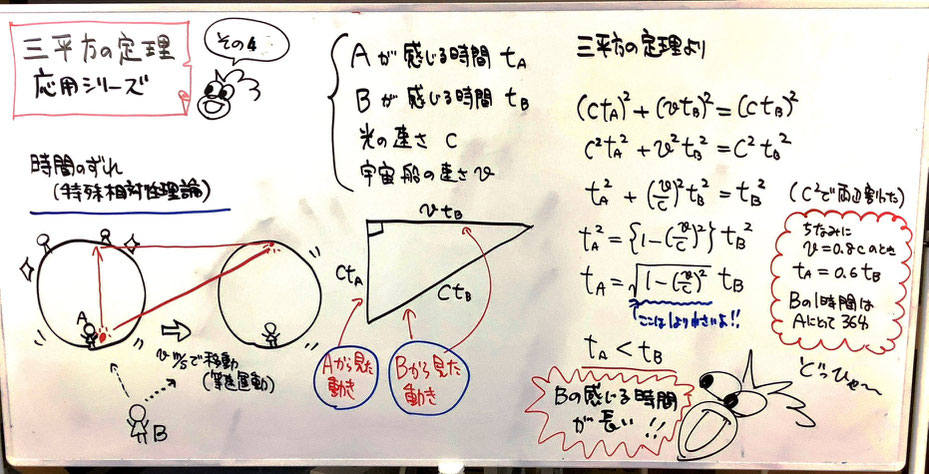
Aが光速に近い速さで運動する飛行体にのって等速運動しています。Aが室内でボールを上に投げ上げます。Aから見たボールの動きはAの真上に伸びる直線上にあります。ところが、これを外から見ていたBは、図の様な斜めの動きで認識します。そこで三平方の定理を使って関係を調べると、Bの感じる時間がAの体感する時間より長いことがわかります。という特殊相対論の定番問題です。

コメントをお書きください