ちょっとおもろい順列の授業

まずは、昨年中学校で行った課外授業からの話題を紹介します。最初に下の写真（左）のように、順列（P）と組み合わせ（C）の関係について、こんなカンジで説明します。「選んでから（C）、一列に並べる（階乗）のが順列（P）」と言いながら、CからPの記号につなげると、生徒も「おお」と納得してくれます。次に順列の基本的な問題を考えるポイントを示したのが下の写真の右の板書です。以下定番問題を解説していくという流れで進んでいきます。

ただ並べ替えるだけでは面白くないので、こんな問題を考えてみました。

次に紹介するのは、私が順列の単元の冒頭の授業で行う内容です。あるお話をして、そこに登場する5人を1列に並べるというだけのものですが、物語仕立てにすることで生徒がくいついてきてくれます。ではまずはそのお話の内容をざっくりと説明しますね。

昔々、ある国にAという村がありました。この村にはマイケルという青年が住んでいました。彼は村に教会をつくったり、学校をつくったりして、村の文化や教育の発展に大いに力を尽くしていました。村人からも尊敬されていました。そんなマイケルには素晴らしい婚約者がいました。その名はリリイ。マイケルの住む村の隣にあるB村に住んでいました。リリイはとても優しく気立てのいい娘さんでした。リリイの家とマイケルの家は遠く離れていましたが、いつもリリイは多忙で村から出かけることができないマイケルに会うために、大きな岩が立ち並ぶ山を越えてA村まで出かけていきました。

 ところがある日、村に突然大雨が襲い、その雨が一ヶ月も降り続きました。この雨によって２つの村の間にあった、岩が崩れ落ち、川が氾濫してしまいました。その後雨は止んだものの２つの村の間には急流の川ができてしまい、行き来することができなくなってしまいました。

来る日もくる日も川を眺めてはため息をついていたリリイでしたが、マイケルに会いたいという気持ちが日に日につのり、なんともしがたくなりました。「ああ。彼に会いたい。でもどうやってこの川を渡ればいいのでしょう。」リリイは近所に住んでいる、大変物知りで手先も器用なきこりのビリイの家を訪ねることにしました。

平和で安泰な村に突然の大災害！２人はどうなるのだろうか。第2話を待て！

リリイはビリイに何とかして川を渡ることができないかと相談しました。するとビリイは川を渡る舟を作ってやろうといいました。しかし川は大変な急流なので、一人で安全に渡るのはとても難しいだろうとのことでした。リリイは何とか一緒に川を渡ってくれないかとビリイに相談しました。しかしビリイは「とても俺にはできない。あそこは水が怒涛のように流れている。命がいくらあっても足りない」といいました。リリイはその言葉を聞いて涙を流しました。その様子を見ていたビリイは、しばらく考えた後、こういいました。「よしわかった。俺は舟は漕げないが、町外れに住んでいるサイモンならできるはずだ。やつは命知らずの冒険野郎なんだ。彼を紹介してやろう」ビリイは、リリイにサイモンを紹介したのでした。

リリイは町はずれに住むサイモンのもとに出かけました。サイモンは「連れて行ってもいいけれど、命がけだぜ。俺だって命は惜しい。タダってわけにはいかないぜ」といいました。リリイはお金ならいくらでも出すといいましたが、サイモンは金はいらないかわりに次のような条件を出しました。

「ようしわかった舟を出そう。ただし条件がある。金はいらねえ。そのかわり、今俺は寂しいんだ。俺と一夜をともにしてくれ。何、煮て食おうってんじゃねえ。一晩だけ俺と一緒ならそれでいいんだ。そのことは誰にもしゃべらねえ。」

リリイは悩みました。悩みに悩んだ末、自分はマイケルに会いたいという気持ちを抑えることができず、サイモンと一夜をともにする決心をしたのでした。

うわあ。サイモンの条件を呑んでしまったリリイ！次回は急展開必至！ 

一夜をともにした2人は翌朝川向こうのマイケルのもとに向かいました。川は大変な急流で、サイモンの見事なオールさばきがなければとうてい渡れるものではありませんでした。何度も舟は転覆しそうになりましたが、サイモンは体を張って凌ぎ、ついに川向こうに舟は辿り着いたのでした。

「ほら着いたぜ．ここはA村の西側だ。ま、ここを道なりにまっすぐに行くとお望みのところに着くだろう。」

サイモンはリリイに言いました。「ありがとうサイモン。ところであなたはまたこの急流を引き返すの？」「ああ。ここにいてもしょうがねえしな。じゃあ、幸運を祈っているぜ。」

リリイの，少し休んでいけばという忠告を無視し、サイモンは再び川を渡り、B村へと引き返しました。リリイはしばらく彼の姿を見ていましたが、はっと我に返りマイケルのもとへと急ぎました。

サイモンは見得を切ってまた川を渡ったのですが、実は疲労はピークにありました。また、リリイには黙っていたのですが、川を渡る際、流れてくる丸太が舟にぶつかるのを防ぐために、足に大きな傷を負っていました。哀れサイモンは力尽きB村に引き返すこともA村に戻ることもできず、濁流に飲まれてしまいました。

そのころマイケルは、この大洪水による被害をなんとかしようと、国王への働きかけを行っていました。早く皆の暮らしが良くなるようマイケルは奮闘していたのです。

リリイはマイケルの家を見つけました。家の前で仕事をしているマイケルを見つけると飛ぶようにして彼のもとにかけつけました。マイケルはリリイの姿を見ると驚きました。「リリイ。ど、どうやって君はあの急流を越えて来たんだ」リリイはなんと答えたらいいか悩みました。悩みに悩んだ末、全部正直に彼に話をしようと決心し、ビリイのことやサイモンのことなど一部始終話しました。

せっかく再び巡り会った２人。しかし・・・破局の予感が．次回怒涛の最終回！

リリイの話を聞いていたマイケルは、しだいに握り締めていた拳がわなわなと震え、そうして両手で頭を抱え、何度も何度もかぶりを左右に振りました。マイケルは怒りを抑えることができなかったのです。「僕と君は時期がくれば結婚することになっている。なのに一体どうしてこんなこと（つまりサイモンと一夜をともにしたことですね）をしなければならないんだ。僕が、この災害を復旧させるために毎日かけずりまわっていたというのに。第一、こんな無茶なことをして高波にのまれて自分の命を失ったらどうするんだああ」マイケルは一気に噴き出しました。そしてもう顔を見せないでくれ、ともいってしまったのです。

リリイは泣き崩れてマイケルの家を出ました。川を渡り自分の家に帰る術もなく、一人村をさまよいあるきました。そのうち、村の東はずれの海岸にたどり着きました。リリイは寄せては返す波に向かって歩き出しました。波しぶきが自分の体や髪をびしょびしょにしましたが、リリイは半ば気を失いかけて、そのまま押し寄せる波に自分をあずけました。

そこに、浜辺近くに住んでいる牛飼いのホームズが通りかかりました。ホームズは浜辺に倒れているリリイを見つけました。「だいじょうぶですか」気を失っているリリイにホームズは声をかけ、とりあえず彼女をホームズの自宅まで連れて帰りました。

「体が冷えている．そうだ温かいスープを作ってあげよう」などと、ホームズはリリイの面倒をよく見てくれました。そのかいがあって、リリイは元気を取り戻すことができました．

その後しばらくして２人は結婚しました．ほどなく２人に子供が産まれました．かわいい男の子だったのでその子供はシモマティ坊やと名づけられました。３人は末永く幸せに暮らしたとのことです。

どんと晴れ．

リリイとマイケルの悲話、いかがだったでしょうか。実はこの話は私のオリジナルではありません。かなり昔に、私がある人から聞いた話を思い出しながら、それを膨らませて書きました。知っている人もいるかもしれませんが、この話はある種の心理ゲームになっています。

　以前この授業を大野高校で行ったとき、就職した卒業生から、新入社員研修でこの話が出たといわれました。盛岡三高では、この物語を数学通信に連載していたら、すごい反響があり、アナザーストーリーを作って持ってくる生徒もおりました。花巻北高校や県外交流先の八戸西高ではこれを読んでくることを宿題にして順列の授業を行いました。ではその授業の様子を以下に記していきたいと思います。

■　Step１　好きな人を1人あげる

この物語には5人の登場人物がいました。リリイ，マイケル，サイモン，ビリイ，ホームズです。さて、この物語を読んだ皆さんは、この5人をどう評価しますか。つまり、この5人をあなたの気持ち、考え方や価値観などに照らし合わせて好きな順番に並べてみるのです。最初に「一番好きな人」を選んでください。そしてその理由も言って下さい（何人かの生徒にあてます。結構盛り上がります）。「さて、好きな人の選び方は何通りでしょう」（当然５通りという答えが返る）

「つまり，５通りの性格分類ができるのです」と言いながら樹形図を描きます。それぞれを選んだ人が何人いるか数えてみます。同じ人物を選んだ人は相性がよいなどというホラを吹いたりします。ランダムに選べば、5人の選ばれる確率は一様分布に従うはずですが、実際には物語を聴いてから選ぶので、かなり偏りのある分布になるはずですね。

■　Step３　好きな順に３人並べる

２人の場合と同じように書き上げていきます。5人から3人選ぶ組み合わせは、(L,M,B)(L,M,S)(L,M,H)(L,B,S)(L,B,H)(L,S,H)(M,B,S)(M,B,H)(M,S,H)(B,S,H)の10通りです。それぞれに対して、その並べ方が６通りだから、１０×６＝６０通りとなります。ここで、「エントリして（つまりＣ）並べるとＰになる」という話（最初にあげた板書の写真参照）とつなげます。樹形図を作ると、３つずつが４束。それが更に５束なので、５×４×３＝６０通りとなります。樹形図を描くのは一見大変そうに思いますが、ひと束を作ったものに対して互換を行えばよいことに気づくとスムーズに行えます。つまり、全部を書き上げる、試行錯誤するという活動によって見えてくるものがあるということです。このような活動を省略して答えだけを与えるのは良い数学的経験が育たないのではないかと私は思います。

■　Step４　好きな順に５人並べる

4人並べる並べ方と、5人並べる並べ方の総数は同じなので、4人は省略して、5人全員を並べる樹形図を頑張って作ってみましょう。樹形図を作ることで、５×４×３×２×１＝120通りであることがわかりますね。作り方は、ひと固まりを作ったら、「M⇔L」「L⇔B」「B⇔S」「S⇔H」といった互換をしていけばいいですね。書きながらそこに気づいていくのが大切です。

こんな風に樹形図を仕上げて、順列（Ｐの計算）の話に進んでいきます。

■　Step５　性格分類

「異なる5人から5人全員選んで一列に並べる並べ方は全部で120通りのパターンがありますね。つまり120パターンの性格分類を行っているのです。タネを明かすと、

リリイ→Lilly →Love→愛　　

マイケル→Mickel→Moral→道徳

ビリイ→Billy→Business→仕事　

サイモン→Simon→Sex→性欲

ホームズ→Homes→Home→家庭　

ということです。例えば、LBMSHと並べた人は、愛を第一に考え、第二に仕事、第三に道徳、第四に性欲、最後に家庭を考えているとなります」（これを明かすとクラスは騒然となります）。

こで注意が必要なのは、サイモン→Simon→Sex→性欲の部分。特に女子で、Sを先頭に書いていたりすると、この話をした後、大急ぎで書き直したりする場合があります。そこで、サイモンは性欲ではなく「冒険心」などとした方がよいかもしれません。

■　Step６　相性率

クラスに40人いると、必ず同じ並べ方をする生徒が少なくとも1組はいます。このことについて確率の余事象の場面で触れてみるのも面白いですね。

さて、ここで問題。今40人のクラスで、このテストを行った時、全部が一致する並べ方になっている人（つまり性格がぴったり一致している人）がいる確率はどのくらいでしょうか。とりあえず、40人がランダムに５つの文字を並べたとします。このときぴったり同じ並びになっている人が少なくとも一組いる確率を計算してみましょう。

まず、40人が全部異なる並べ方になっている確率を考えます（余事象ですね）。もし人数がA,B,C の3人だとすると、BはAの並べ方以外の119通りのどれか、CはA，B以外の118通りのどれかなので、3人とも異なる並びになる確率は、

ちなみにこれを計算すると、約0.975なので、少なくとも1組が一致する確率は1－0.975＝0.025　ということで、ほぼ２.5％ということになります。では40人のときはどうなるでしょう。全部異なる場合の確率は、

となりこの値を計算すると約0.00042となります。ということは，40人の中で少なくとも1組が同じ並びになっている確率は

１－0.00042＝0.99958

つまり、99.96％の確率で同じ並びの人がいるといえます。ほとんど100％といってもいいですね。ちなみに、半分の20人の場合でも、84%という高い確率になります。参考までに、2人から40人までの、少なくとも一組が一致する確率の分布は次の表のようになります。

この話は、誕生日の一致の確率の問題としてよく話題になりますね。ちなみに、40人のクラスで誕生日が同じ人が少なくとも1組存在する確率は、

つまり、40人いればほぼ90%の確率で同じ誕生日の人がいるということがいえるのですね。

■　Step７　一致の問題（全換置換）

今度は2人一組になって2人の相性を調べてみましょう。冗談で、こんな相性率の表を見せたりします。

この表のそれぞれの場合の確率は次のような樹形図を用いて求めます。

全部一致するのは1通り。

４か所だけ一致する場合はありえません（4か所一致すれば必ず5か所一致する）。3か所だけ一致するのは、どの場所が一致するかが 5C3 通りで、それぞれ１通りの一致しない仕方がありますから、総数は10×1＝10通り。2か所だけ一致するのものは、どこが一致するかが 5C3 通りで、それぞれに対して2通りの一致しない仕方があるので、総数は10×2=20通り。同様にして、1か所だけ一致するのは、5×9＝45通りとなります。すると、余事象の考えから全く一致しない確率は、

となりますね。ちなみに、この確率の逆数を計算すると、

30/11＝2.72727･･･となります。

これは自然数の底eの値に近いですね。それについて少し補足したいと思います。

5つが全部一致しない場合の数は次のように考えることができます。まず全体から、１つ以上一致する場合の数を引きます。これだと引きすぎなので、2つ以上一致する場合の数を足します。今度は足しすぎになるので、3つ以上一致する場合の数を引きます。そうやって計算した式が次のものです。

私はこれを「引きすぎ足しすぎ論法」と呼んでいます。わかりにくいと思うので、３つの場合で考えてみましょう。

下のベン図をご覧ください。

そこでこれを一般化して、ｎ個の異なるものを一列に並べたとき、一つも一致しない確率は次のようになります。

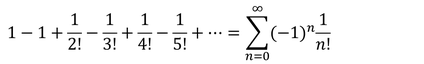
ここで、次の指数関数のべき展開の式が想起されます。

つまり、ｎ個の列が全く一致しない確率（全換置換）の確率は1/eの（結構早い）近似になっているということですね。

かなり以前になりますが、北海道で行われたある講座で先生方を相手にこのお話をしました。そのダイジェスト動画をあげておきます。よかったらご覧ください。