shiawase2021というオンラインイベントでお話しした内容について、ブログにまとめています。
「あなたと夜と数学と」では2021年3月20日にアップしたものです。よかったらご覧くださいね。
幸せ×数楽

国際幸福デーの今日から、shiawase2021のビッグイベントがオンラインで行われております。20・21日と行われるわけですが、ちょうどこれが2021にかかっていますね。
私は、キャリアクエストの齋藤みずほさんと80分ほどのワークショップ『幸せ×数楽(ウェルビーイング・カフェ®)幸せについて対話してみよう!』を先ほど行っておりました。
幸せ感あふれる参加者のおかげで楽しい時間を共有することができました。「あなたとハピネスと数学と」というテーマで私が話した3つのことを以下にまとめます。
足し算と引き算とハピネスと
最初に、算数の足し算と引き算と幸せについての話をしたいと思います。皆さんは、「足し算と引き算」と聞いて、どちらに「幸せ」のイメージを抱きますか?
足し算の方が「増える」というポジティブな印象を受けますし、引き算は「減っていく」ということで何となくネガティブなイメージを持つので、足し算の方に「幸せ」のイメージを抱くかもしれませんね。
でも私はあえて、引き算の幸せについて話してみようと思います。足し算型の幸せというと、人よりお金を稼いでいるとか、人よりテストの成績が良かったとか、高い地位を得たとか・・、いわばたくさんのギフトをもらって、気持ちが良くなった状態と言えると思います。でも、このような「幸せ」「満足」は、わりともろいのではないか、あまり持続しないのではないかと私は思うのです。
テストでいい点を取っても、自分より上の人がいると、その満足は崩れます。お金をいっぱい稼いでも、使ってしまえばその満足は消えてしまいますし、隣の人が自分よりもっと稼いでいれば悔しい気持ちになるでしょう。会社で課長に出世しても、自分より若い人がもっと大きな部署で課長に昇進したら、その幸せ感は一瞬にして消滅し、ジェラシーの炎が生まれるかもしれません。
このような足し算型の幸せを分析すると、そこには何か、他者との比較の中で得る優越感のようなものがあるように思えます。他者性・相対化という視点です。しかも、その優越感の根拠が曲者です。その優越感とか、幸せだと思う根拠や価値観はどこから来ているのかというと、例えば周囲に対する見栄だったり、承認欲求だったり、単に世間がそういっているからという、古き習慣や伝統、あるいは家庭や学校教育などで刷り込まれた価値観だったりするわけです。
例えば、偏差値の高い学校=いい学とか、いい高校、いい大学からいい会社に入って、それが幸せな人生、とか。自分というものの多くは「他人の思想や言葉」によって作られています。そして、それが無意識に自分の信念だと思ってしまっているという状況があります。幸せに生きるには、それを捨て去る(引き算)ことこそが大切なのではないかと私は思います。
引き算の幸せについてもう一つ付け加えておきます。以前、みずほさんから選択理論心理学における「感覚、知識、価値」バイアスという話しを伺ったことがあります。人は、ある状況に直面したとき、行動が選択されるわけですが、みずほさんは、その瞬間に選択される行動の集合体を「タンスの引き出しにしまわれたモノ」と例えられました。
私たちは行動を選択する際に、無意識に、タンスの引き出しの一番取りやすいところに手を出してしまいがちです。例えば、「批判する」「責める」「文句を言う」などという反応ですね。で、その根拠となるのが、他者によって作られ身体化されてしまった価値観という一面もあると私は思うんです。
そういう情動を引き算して整理すること、それがwell-being、whole-being、幸せな状態を常態化することではないかと思います。そういう引き算している人は、「楽しい」「充実感がある」「集中できる」という状態にいるわけで、それこそがまさに幸せであるということかなと思うんです。その状態にいることで、気がついたら夢や目標が叶っていると。つまり、最初から目標をゲットすることに向かわないんですね。目標をゲットした、だから幸せ、ではなくて、幸せな状態でいる、すると期せずして目標がついてくる、というカンジですね。
微分とハピネス
次に微分と幸せの話をしたいと思います。数学の言葉では「ベクトル」とかは、社会的に流通しているような気がします。例えば「ベクトルを揃えて頑張りましょう」とか。でも、「微分」という言葉は日常的にはほとんど使われていませんよね。使われるとすると、難しいモノの象徴という文脈で登場するカンジです。ま、微分って「微かに分かる」、積分は「分かった積り」と書くわけですが。実は私は、微分という言葉をもっと日常で使おうと提案しているんですよ。
さて、微分を考えるためには、まず関数を定義しなければなりません。中学高校で教える関数とは、おおざっぱにいうと「ともなって変わる2つの量x、y」があったときのxからyへの対応のことです。例えば、自動車を運転するとき「移動距離y」は「時間x」の関数と考えることができます。関数はy=f(x)という式で表され、それを座標平面にグラフで表すことで、変化の様子を見える化することができます。ここで、f(a) とは、x=a のときの関数の「値」のこと。f'(a) とは、x=a の瞬間の「変化率」のことで、これをx=a における微分係数といいます。グラフでいうと、接線の傾きになりますね。
少し飛躍した言い方になりますが、私は、この「微分」を、その時点における「伸びようとする強さ」「追いかける勢い」というように捉えたいと思います。そしてこれを更に「内包するエネルギー」とか「内に秘めたポテンシャル」というように発想を飛ばしてみたいのです。
関数において、ある時点での様子を考えるということは、その時の値はいくつなのかということと、その瞬間にどの方向に向かっているか(このままいくとどのような方向に進むか)という2つの面から捉えていく必要があります。一つ例を挙げたいと思います。プロ野球のロッテの佐々木朗希投手と、ジャイアンツの菅野投手のどちらかが大リーグのチームにスカウトされるとします。どちらの投手が高い評価を受けるでしょうか。投手としての実績を数字としてみると、登板数、勝利数、奪三振数、完投数
いずれも菅野の方が上です。佐々木投手の実績はほぼゼロですよね。それをもって菅野が佐々木より高い評価を受けるのは、関数でいうと「関数の値を評価した」ということになるでしょう。
しかし、佐々木投手をとりたいとする人もいるでしょう。それは「現時点における将来への可能性」を菅野投手より高く評価しているという考え方だと思います。現時点での伸び率の比較というのはまさに「微分係数の比較」による評価ということです。
先日ある高校の先生がフェイスブック「大切なのは点数ではない、成長できたかどうかだ」と書いていましたが、点数というのは「関数の値」、成長とか学びに向かう姿勢というのは「微分」というカンジですね。

前置きが長くなりましたが、ここで幸せについて考えてみたいと思います。横軸を時間、縦軸をゲットしたギフトの量としてA,B,Cの3人のある時間の状態を点で示します。Aの値が一番大きいですね。ではAが一番幸せといっていいでしょうか。

ここでグラフの変化のようすを見ると、次のようになっていました。Aは確かに値は大きいけれど、下り坂の状態にあります。一方Cは一番ギフトは少ないけれど微分係数は一番大きいですね。
私は、幸せとは、ギフトの量の多さではなく、その変化の割合(つまり微分)の方に関わるものではないかと思います。皆さんはどのように考えられますか。
ここで、今度は微分方程式の話をしたいと思います。心理学で「フェフィナー・ウェーバーの法則」と呼ばれるものがあります。感覚の変化量は、現在の刺激に反比例するという法則です。
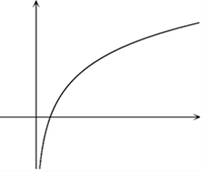
例えば、ロウソクが3本から4本に増えたときの感覚(驚き)の変化は、100本から101本に増えたときと比べてずっと大きいということですね。ここで、 y を感覚 x を刺激として、これを式で書くと、dy/dx=k/x という微分方程式になります。
この微分方程式を解くと、左の図のようなグラフで描ける対数関数が得られます。
私は幸せの感じ方もこれかもしれないなかと思うんです。ギフトを持たざる者こそ、幸せを感じる感度が高く、お金も、地位も、名誉もいっぱい持っている人は小さなモノに幸せを感じない。これはちょっと語弊があるので言い直すと、「こうあるべき」という人から植え付けられた信念とか「世間への承認欲求とか」そういう虚飾にまみれている人は、幸せの感度が低くて、そういうものを引き算によって整理し、スリムになっている人は歩いているときに見つけた小さな花にも幸せを感じる、そんなカンジかもしれません。
数学は最適を求める旅

写真1

写真2

写真3
最後に、数学とは何かというスケールの大きい話をしたいと思います。数学とは自然現象の秘密を解くための学問でもあります。こんな例をご紹介したいと思います。
上の写真1は、円形の輪に石鹸幕を張ったものです。輪が中にできるように糸をわたしています。今、その石鹸膜の内部にある糸の輪で囲まれた部分を針でつついて、石鹸膜に穴をあけます。すると写真2のようにきれいな円形の穴があきます。
完璧な円です。石鹸膜は、どの部分も、同等な張力で張られています。だから輪の中に穴があくと、外側の膜が引っ張る力によって、内部の輪は、面積を最大にしようという現象がおきるのでしょう。糸の長さが一定なので、その中で最大の面積を持つ図形が円というわけです。言い換えると、同一面積の図形の中で周の長さが最も短い図形が円なので、円に落ち着くといってもいいかもしれません。
写真3は、寒い冬に、猫がまるで球体のように丸くなっているものです。なぜこのようにするのでしょう。猫は気温が下がると、体温をできるだけ放出したくないために、体の表面積をできるだけ小さくしようとします。球とは、決まった体積を覆う、最小の表面積を持つ物体だからです。まるで石鹸膜も猫も数学を知っているかのようです。
以前、「やまとなでしこ」というテレビドラマの中で、「数学や物理というのは神様のチェスを横から眺めてそこにどんなルールがあるのか。どんな美しい法則があるのか探していくことだ」という、物理学者のリチャードファインマンの言葉が紹介されていました。自然現象とは、でたらめに起こっているものではなく、「エネルギーが最小の状態で安定する方向に推移していく」という原理(変分原理)が働いていると推察できます。いわばそれが「神様が行っているチェスのルール」でしょうか。
私は数学の授業の中で、生徒に「数学とは最適を求める旅」と言っています。実際、数学では最大値や最小値を求める問題が多く登場します。私は、数学の問題解決とは、どうすれば最適な解に到達できるかについて、様々な視点から考察し、試行錯誤し解決に向かっていこうとすることだと思っています。そしてそれは、数学という教科を超えて、世の中の不合理に対してきちんと批判の目を向ける力になったり、あるいは、より幸せに生きるにはどうするかといった、「より良くしよう」精神につながることだと生徒たちには話しています。
先ほどの石鹸膜、完璧な円になることに驚かされます。それは、限られた長さの糸の中での最大面積、つまり石鹸膜にとって最高の幸せな状態を自ら生み出そうとした結果なのだと私は思います。こざかしく振る舞うのではなく、自然のまま、あるがままに居続けることが幸せなこと。猫も同様です。球が最適であることなんて猫は知りません。でも、幸せな状態になろうとすると、そこに美しいフォルムが自然に生まれるのです。
ならば、人間も、今置かれている環境の中で、最適な自分を見つけることが幸せなことであり、他者の言葉、人の評判、自分の中にある誰かによって作られた声そんな様々な雑音は、本来自然にできるはずのまん丸の円を「いびつな円」にしてしまいます。本当は人も猫や石鹸膜同様、完全な円を作っていたはずなんです。
自分が最初から持っている「円」や「球」に立ち戻るためには引き算をしていくことが大切だ。答えは自分自身と自然の中にあるんだ。私は石鹸膜や猫から学んだ思いをしたのでしたした。
何か壮大な話になってしまいました。皆さんはどんなことを考えますでしょうか。

コメントをお書きください