今回のブログの内容は、2020年5月9日にブログ「あなたと夜と数学と」に書いた「Covid-19における均衡モデル」をまとめなおしたものです。どうぞよろしくお付き合いくださいませ。
昨日、床に伏しながら、ぼんやりとCovid19の感染における均衡モデルのようなものを作れないか考えていました。そこでWebにあたったら、古典的なものでありますが、SIRモデルという微分方程式で表される決定論型モデルを見つけることができました。でもこれはちょっと難しそうなので、それを参考にしつつ、自分なりに離散力学系のモデルを考えてみました。
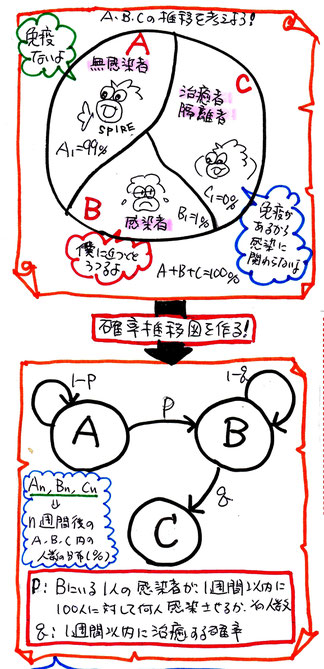
まず、A群(無感染者)B群(感染者)C群(治癒者・隔離者)とカテゴライズし、その遷移図から漸化式を作ります。
(右図参照)
でもこれはちょっと難しそうなので、それを参考にしつつ、自分なりに離散力学系のモデルを考えてみました。
(下図参照)

これをエクセルで表現したのが下の図です。
ちなみに初期値はA1=99 B1=1 C1=0 としています。つまり、1%の感染者がいるという状態です。まあ、大したことのないものではありますが、数字を変化させると結構いろいろなことが見えてきます。2つほど気づいたことをまとめておきたいと思います。
1 qを固定してpを変化させる
q(1週間以内に治癒する確率)を50%に固定し、pを2.0人から1.1人まで変化させてみます。GIFアニメを作りました。(右図参照)
pが大きいほどピークアウトは早いですね。しかし、p>1.5人だと、人口の40%以上が罹患するので医療崩壊になります。
人のつながり(経済活動も含め)を活性化させると、終息は早いけれど犠牲が伴うことがわかります。P=1.1人だとほぼ10週間でピークアウトしその後緩やかに均衡しますし、C群も20%を下回ります。

2 pを固定してqを変化させる
今度は、pを1.5人に固定して、qを25%から70%まで上げていきます。(右図参照)
すると、B群のピークの時期は変化しませんが振幅が減少してくことがわかります。q=70%だと、ピークは20%程度に落ち着きます。
qを高めるには、劇的な治療法やワクチンの開発などが待たれるわけですが、それがまだ先にある段階でできることは、隔離を進めることであることに気づかされます。
つまり、PCR検査の数を増やして感染者になりうる人を隔離していく戦略が重要ではないかと感じられます。

以上、私のいいかげんなまとめでありますので、間違い勘違いが多々あるかと思います。ご容赦のほどを。


コメントをお書きください